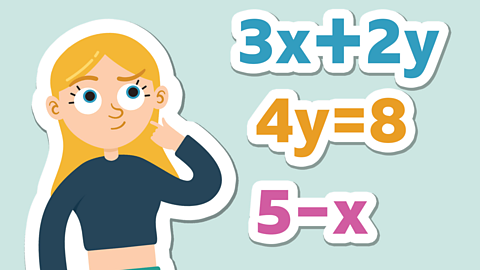����ý

If you enjoy solving puzzles, you are going to love algebra!

Algebra is used in Maths when we do not know the exact number or numbers in an equation. In place of these missing numbers, we use letters or symbols. For example, 6 + x = 13.

The same digits from this number sentence can be used, in a different order, to find out the missing number (x).

In this case, x stands for 7 because 13 – 6 = 7.

You may also see an equation written as 2y = 6.

This means 2 sets of y = 6, so to find 1 lot, we divide by 2 and find that y = 3.

Algebra can also be a very useful way of remembering important formulas, such as those for finding the area or volume of a shape.

If we know that a square has four sides measuring 8cm each, we can follow the formula:A = W x H (Area = Width x Height) to calculate the square’s area: 8cm x 8cm = 64cm2.

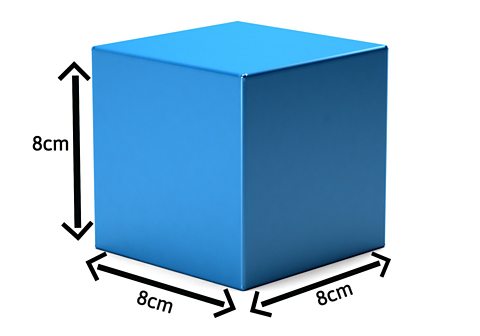
If this square was a cube, we would need a new formula to measure its volume:

V = (W x H) x L or Volume = (Width x Height) x Length.

From this, we can see that the volume of the cube is:

(8cm x 8cm) x 8cm = 512cm3.

Understanding algebra is a very important skill when working with function machines.

The dictionary tells us that a machine is a device that carries out a task. Some machines, like forklifts and lorries, make lifting and moving things easier; others, like telephones and computers, allow us to speak to people anywhere in the world. Even in school, we are surrounded by helpful machines everyday – you just have to take a look around your classroom!

Now, think about the last time you bought something from a vending machine, maybe your favourite chocolate bar or an ice-cold drink. Have you ever thought about how it all works?

The idea is actually very simple: first, you put your money in; then, you type in the code of the item you want and finally, the vending machine gives you your treat.

The vending machine is performing a function – it is following a set of rules based on the information you have given it to provide you with food at the end.

How does this apply to maths?

This same idea is also applied in mathematics through the use of function machines. We use function machines to show the order in which rules (the function) should be carried out to a given number or value (input – just like the money you placed in the vending machine) to produce a result (output – your treat).

By picturing all three steps as one machine, it becomes a lot easier to follow and understand, much like a flowchart. The rules for functions can be as simple or as complicated as you like, but to be a real function machine they must be consistent so that every time you give it the same input, you get the same output, with only one possible answer each time.

For example: INPUT: 3 FUNCTION: + 3 OUTPUT: = 6.

It is also possible to connect two function machines together to make a ‘network’.

By doing this, the output from the first machine feeds straight back into the output of the second. For example:

• First machine
  • INPUT: 3 FUNCTION: + 3 OUTPUT: = 6
• Second machine
  • INPUT: 6 FUNCTION: x 2 OUTPUT: = 12

Function machines can also be used to help us find solutions to problems where the input or function are unknown. By following the same steps, in a different order, we can use our thinking skills to find the solution. See if you can work out the answer to the example below.