Key points
In order to work with gradients and straight lines successfully, a good understanding of coordinates and linear graphs is needed.
The gradientA measure of the slope of a line. The steeper the line, the greater the gradient. The gradient is represented by ØÆÄ in the equation ØÆÜ = ØÆÄØÆÖ + ØÆä is a measure of slope. The greater the gradient, the steeper the slope.
When the gradient of two lines are the same, they are parallelAlways equidistant (at equal distances). Parallel lines, curves and planes never meet however far they extend. . When the gradients have a productThe result of multiplying two or more terms. of -1, they are perpendicularPerpendicular lines are at 90┬░ (right angles) to each other. .
The gradient of a line is calculated by dividing the difference in the \(y\)-coordinates by the difference in the \(x\)-coordinates. This may be referred to as the change in \(y\) divided by the change in \(x\), or the vertical divided by the horizontal.

Understanding the gradient of a straight line
The gradient is the amount of verticalThe up-down direction on a graph or map. movement for each unit of horizontalThe right-left direction on a graph or map. Parallel to the horizon. movement to the right. The greater the gradient, the steeper the slope.
A positive gradient slopes up from left to right. A negative gradient slopes down from left to right.
A gradient of 2 and a gradient of -2 have the same steepness. A gradient of 2 slopes up from left to right, and a gradient of -2 slopes down from left to right.
Parallel lines have the same gradient.
Perpendicular lines are sloped in opposite directions. One has a positive gradient and the other has a negative gradient. The product of their gradients is -1
Examples

Image caption, The gradient is a measure of the slope of a line. It is the amount of vertical movement for each unit of horizontal movement to the right. The greater the gradient, the steeper the slope. The gradient of 3 is steeper than the gradient of 1 and the gradient of 2
Image caption, A positive gradient slopes up, from left to right. A negative gradient slopes down, from left to right.
Image caption, These lines have the same steepness. When each unit of horizontal movement to the right has a vertical movement of two up, the line has a gradient of 2. When each unit of horizontal movement to the right has a vertical movement of 2 down, the line has a gradient of -2. A gradient of 2 and a gradient of -2 have the same steepness, one going up and the other going down, from left to right.
Image caption, Parallel lines have the same gradient. Both lines have a positive gradient. Here, each unit of horizontal movement to the right has a vertical movement of 3 up. Both lines have a gradient of 3, they are parallel.
Image caption, To show that lines are parallel, arrow notation is used.
Image caption, Perpendicular lines are sloped in opposite directions and their gradients have a product of -1. Here, one line has a positive gradient of ┬¢ and the other has a negative gradient of -2. The product of their gradients, ┬¢ ├ù ÔÇô2, is -1
Image caption, Decide whether any two of these lines are parallel or perpendicular.
Image caption, Lines that are parallel have the same gradient. These lines all have different gradients. None of these lines are parallel.
Image caption, Lines that are perpendicular are at 90┬░ to each other. They slope in opposite directions, one has a positive gradient and the other has a negative gradient. The product of their gradients is -1, which means their gradients multiply to -1. Two of the lines, ØÆÜ = 4ØÆÖ +3 and ØÆÜ = ØÆÖ/4 + 3, have positive gradients and so they cannot be perpendicular. One line, ØÆÜ = 3 - 4ØÆÖ, has a negative gradient. Each positive gradient is multiplied by the negative gradient to find if any product is -1. ┬╝ ├ù -4 = -1. Therefore the lines ØÆÜ = ØÆÖ/4 + 3 and ØÆÜ = 3 - 4ØÆÖ are perpendicular.
1 of 9
Question
Which of these lines have the same gradient?
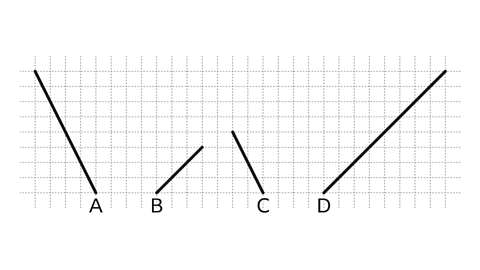
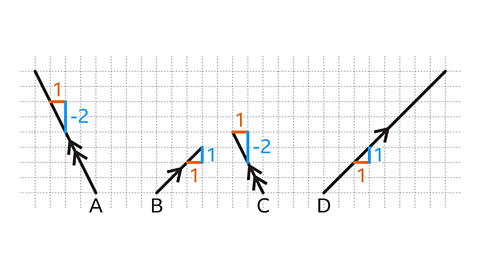
A and C have the same gradient. For each unit of horizontal movement to the right the vertical movement is -2 (2 down). They are parallel.
B and D have the same gradient. For each unit of horizontal movement to the right the vertical movement is 1 (1 up). They are parallel.
Working out the gradient of a straight line on a graph
To work out the gradient of a straight line:
Choose two points on the line.
- Any two points will work.
- Whole numbers make the working easier.
Draw a triangle showing the horizontal movement to the right and the vertical movement (up or down).
Label the triangle with the change in the \(x\)-coordinate and the change in the \(y\)-coordinate.
Work out the value of the change in the \(y\)-coordinate divided by the change in the \(x\)-coordinate.
Examples
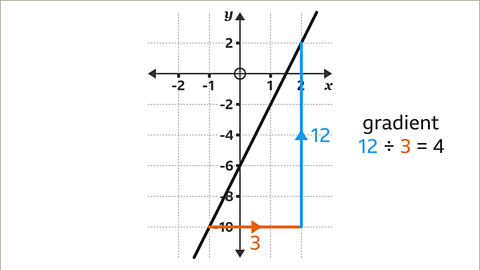
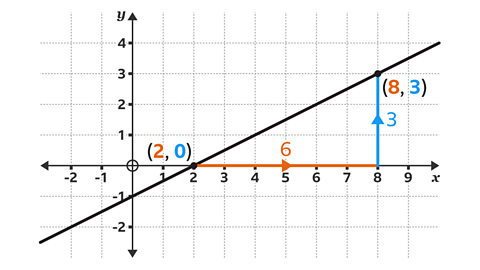
Image caption, The gradient is the change in the ØÆÜ-coordinate divided by the change in the ØÆÖ-coordinate.
Image caption, Two points (8, 3) and (2, 0) have been chosen. Use these coordinates to find the gradient of the line.
Image caption, Draw a triangle showing the horizontal movement to the right and the vertical movement up. Label the triangle with the change in the ØÆÖ-coordinate (6 steps across the ØÆÖ-axis from 2 to 8 is 6) and the change in the ØÆÜ-coordinate (3 steps up the ØÆÜ-▓╣│µ¥▒▓§ from 0 to 3 is 3).
Image caption, Work out the gradient, the value of the change in the ØÆÜ-coordinate (3) divided by the change in the ØÆÖ-coordinate (6). 3 ├À 6 = ┬¢. The gradient of the line is ┬¢
Image caption, A gradient of › means that the vertical movement is › for each unit of horizontal movement to the right.
Image caption, Work out the gradient of the line.
Image caption, Choose two points on the line, any two points will work. Whole numbers make the working easier. (-1, 7), (0, 4), (1, 1) and (2,-2) are suitable.
Image caption, The two points used here are (0, 4) and (1, 1). Draw a triangle showing the horizontal movement to the right and the vertical movement down. Label the triangle with the change in the ØÆÖ-coordinate (from 0 to 1 is 1) and the change in the ØÆÜ-coordinate (from 4 to 1 is -3).
Image caption, Work out the gradient, the value of the change in the ØÆÜ-coordinate (-3) divided by the change in the ØÆÖ-coordinate (1). -3 ├À 1 = -3. The gradient of the line is -3
Image caption, Any two points will give the same gradient. Using the points (-1, 7) and (2, -2), the change in the ØÆÜ-coordinates (-9) is divided by the change in the ØÆÖ-coordinate (3). -9 ├À 3 = -3. The gradient of the line is -3
1 of 10
Question
Work out the gradient of the line.
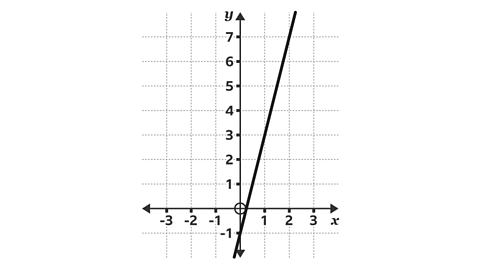
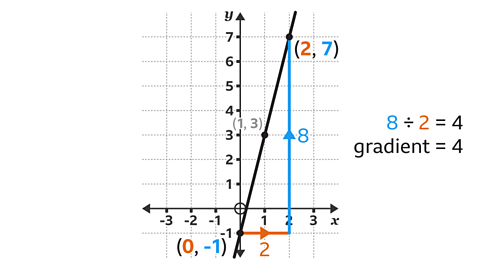
There are three points to choose two from, (0, -1), (1, 3) and (2, 7).
Using (0, -1) and (2, 7), draw a triangle showing the horizontal movement to the right and the vertical movement down.
The change in the \(y\)-coordinates (8) is divided by the change in the \(x\)-coordinate (2), 8 ├À 2 = 4
The gradient of the line is 4
For a different pair of coordinates, (0, -1) and (1, 3) or (1, 3) and (2, 7), the change in the \(y\)-coordinates (4) is divided by the change in the \(x\)-coordinate (1), 4 ├À 1 = 4
The calculation gives the same answer.
Finding the gradient and intercept
The equationA mathematical statement showing that two expressions are equal. The expressions are linked with the symbol = of a straight line can be written as \(y = mx + c\)
- \(m\) is the gradient.
- \(c\) is the \(y\)ØÆÜ-¥▒▓È│┘▒░¨│ª▒▒Þ│┘The point at which the line crosses the ØÆÜ-▓╣│µ¥▒▓§. Commonly referred to as 'the intercept'..
To write the equation of a straight line:
- Work out the gradient.
- Find the \(y\)-intercept, the value at which the line crosses the \(y\)ØÆÜ-▓╣│µ¥▒▓§The line on a graph that runs vertically (up-down) through the origin. It is used as a reference to measure from..
- Write the equation in the form \(y = mx + c\)
Example

Image caption, Find the equation of the line.
Image caption, First, find the gradient of the line. Choose two coordinates on the line. Here (-1, 4) and (1, -2) have been chosen. Draw a triangle showing the horizontal movement to the right and the vertical movement down. Label the triangle with the change in the ØÆÖ-coordinate (from -1 to 1 is 2) and the change in the ØÆÜ-coordinate (from 4 to -2 is -6).
Image caption, Work out the value of the change in the ØÆÜ-coordinate divided by the change in the ØÆÖ-coordinate. This gives -6 ├À -2 which is -3. The gradient of the line is -3
Image caption, Now find the ØÉ▓-intercept of the line. The value where the line crosses the ØÉ▓-axis is 1
Image caption, Write the equation in the form ØÆÜ = ØÆÄØÆÖ + ØÆä where ØÆÄ is the gradient (-3), and ØÆä is the ØÆÜ-¥▒▓È│┘▒░¨│ª▒▒Þ│┘ (1). The equation is ØÆÜ = -3ØÆÖ + 1. This may also be written as ØÆÜ = 1 ÔÇô 3ØÆÖ
1 of 5
Question
Work out the equation of the line.


Choose two coordinates on the line. Here (1, 4) and (3, 10) are used.
Draw a triangle showing the horizontal movement to the right and the vertical movement up.
Label the triangle with the change in the \(x\)-coordinate (from 1 to 3 is 2) and the \(y\)-coordinate (from 4 to 10 is 6).
Work out the value of the change in the \(y\)-coordinate divided by the change in the \(x\)-coordinate. This gives 6 ├À 2 which is 3. The gradient of the line is 3
Find the \(y\)-intercept of the line. The value where the line crosses the \(y\)-axis is 1
Write the equation in the form \(y = mx +c\) where \(m\) is the gradient (3), and \(c\) is the \(y\)-intercept (1). The equation is \(y = 3x + 1\)
Practise working out the gradient of a straight line
Quiz
Practise reading and plotting quadratic graphs with this quiz. You may need a pen and paper to help you with your answers.
Real-life maths
The gradient of a line gives the rate of change.
Although graphs in real life may not always be straight lines, the principle of using gradients as a rate of change is useful.
Scientists, such as physicists, might carry out experiments where they need to track the distance a particlesAll substances are made of particles. Particles could be atoms, molecules or ions. travels over time. They could use a graph to show this and the gradient of the graph would show the speed of the particle.


Understanding gradient is important for architectA person who designs and draws plans for buildings. when calculating the slope of a roof, otherwise known as the roof ÔÇÿpitchÔÇÖ.
There are rules and regulations for how steep a roof can be.
For example, if the steepest incline allowed for a house extension is 15┬░ (this is a gradient of approximately 0█░268), this will have an impact on the distance that the extension can be built out to the original walls of the house.

Game - Divided Islands
Play the Divided Islands game! gamePlay the Divided Islands game!
Using your maths skills, help to build bridges and bring light back to the islands in this free game from ┤¾¤¾┤½├¢ Bitesize.

More on Graphs
Find out more by working through a topic
- count6 of 7
- count7 of 7
- count1 of 7
- count2 of 7
