Key points
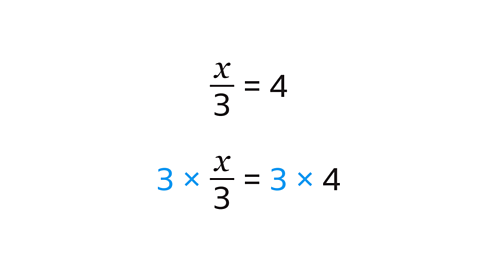
- An A mathematical statement showing that two expressions are equal. The expressions are linked with the symbol = is like a set of scales that are in balance. The An element within an algebraic sentence. Elements (terms) are separated by + or - signs. on either side of the equals sign (=) have the same value as each other.
- Solving equations becomes easier when the number of terms is reduced.
- Equations need to stay in balance. Whatever is done to one side of the equation must also be done to the other. For example, multiplying or dividing each side of the equation by the same value.
- It is useful to know that \(\frac{1}{2}\)\(饾挋\) is the same as \(\frac{x}{2}\) and \(\frac{1}{5}\)\(x\) is the same as \(\frac{x}{5}\), whereas \(\frac{3}{4}\)\(x\) is the same as \(\frac{3x}{4}\)
- Usually, A number that we do not know. They are commonly used in algebra, and sometimes referred to as variable and represented by symbols such as 饾挋 or 饾挌 are given a value of \(x\), however any letter can be used to represent an unknown value.
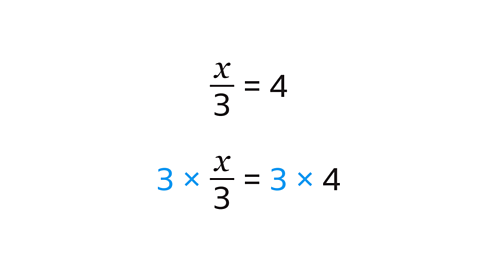
Equations involving one fraction
- If an equation has just one fraction, then the most common first step is to multiply both sides by the Number written on the bottom of a fraction. The denominator is the number of equal parts. Eg, for 1鈦3, the denominator is 3 of the fraction.
- Multiplying both sides of the equation will remove the fraction.
- The number of terms will be reduced and will lead to a new equation that is still balanced.
- The new equation will have just one unknown A quantity that can take on a range of values. .
- Solving equations becomes easier when the number of terms is reduced.
- Check your answer by In algebra substitute means to replace a letter (or variable) with a number. the solution back into the original equation.
Example
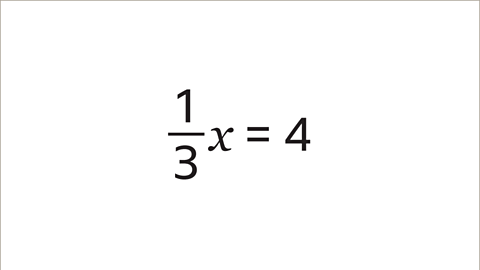
Image caption, Solve the equation 鈪擆潚 = 4 by working out the value of 饾挋
1 of 6
Question
Find the value of the unknown term \(x\) in this equation.
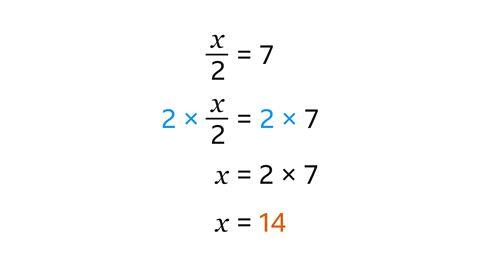
Multiply each side by 2, meaning \(x\) = 14
Check your answer by replacing \(x\) with 14
If \(x\) = 14, then 14 梅 2 = 7
When \(x\) = 14, both sides of the original equation are equal.
This confirms that \(x\) = 14
Equations with fractions on both sides
Equations involving fractions on both sides need to be simplified by multiplying both sides by an appropriate number to keep the equation balanced.
- Find the The lowest multiple that is common to two or more numbers. The LCM of 15 and 12 is 60 because it is the lowest value in both of their multiplication tables. Also known as the least common multiple. (LCM) of both Number written on the bottom of a fraction. The denominator is the number of equal parts. Eg, for 1鈦3, the denominator is 3.
- Multiply both sides of the equation by the lowest common multiple.
This will reduce the number of terms and lead to a new equation that remains balanced.
Example
Image caption, Solve the equation by working out the value of 饾挋.
1 of 9
Question
Find the value of the unknown term \(x\) in this equation.
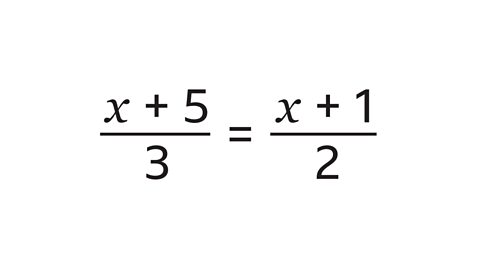
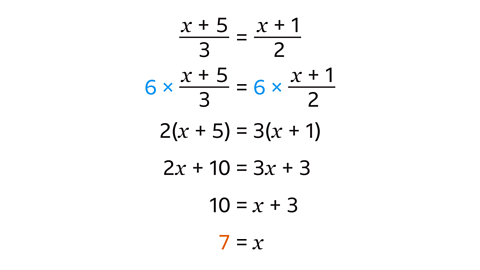
Multiply both sides by 6, the LCM. This leaves 2(\(x\) + 5) = 3(\(x\) + 1)
Expand the brackets: 2\(x\) + 10 = 3\(x\) + 3
Subtract 2\(x\) from both sides: 10 = \(x\) + 3
Subtract 3 from both sides: 7 = \(x\)
Check the answer \(x\) = 7 in the original equation: If \(x\) = 7, then (7 + 5) 梅 3 = 4 and(7+1) 梅 2 = 4
When \(x\) is 7 both sides of the equation are equal.
This confirms the solution \(x\) = 7
Practise solving equations using fractions
Quiz
Practise solving equations with fractions with this quiz. You may need a pen and paper to help you with your answers.
Game - Divided Islands
Play the Divided Islands game! game
Using your maths skills, help to build bridges and bring light back to the islands in this free game from 大象传媒 Bitesize.
More on Equations
Find out more by working through a topic
- count5 of 7
- count6 of 7
- count7 of 7
- count1 of 7
