Problem 6 - Sequences
Problem 6 is all about sequences and finding missing information.
Maths teacher Chris Smith and pupils from Grange Academy are here to explain.
The Maths Week Scotland Daily Challenges have been set by the Scottish Mathematical Council.
CHRIS: This challenge is all about sequences. A sequence is an ordered list of numbers that follow a pattern. There are two parts to this question so listen carefully.
Part A.
A simple sequence can be made starting with three and adding four each time: three, seven, eleven, fifteen, nineteen and so on. What do the first six numbers of this sequence add up to?
And it goes up in fours. So we'd have a three, then a seven.
Part B.
This part is about a different sequence of the same type, but we don't have all the information. The first number in this sequence is five and the sum of the first six numbers is one hundred and twenty. Using the information given, can you work out what the second number in the sequence is?
Explain your answer.
And I'm not gonna tell you what it goes up in and so what I want to know, what would the second term in this sequence be?
PUPIL: Remember that you always add the same amount to get to the next number in the sequence.
PUPIL: Don't forget that each number is made by adding an amount to five.
PUPIL: Try using algebra to make an equation.
PUPIL: Can I use algebra to work this question out?
CHRIS: Yeah. Algebra would be a great way to attack this question.
PUPIL: Good luck.
Part A
A simple sequence can be made starting with 3 and adding 4 each time:
3, 7, 11, 15, 19 and so on
What do the first six numbers of this sequence add up to?

Part B
This part is about a different sequence of the same type but we donāt have all the information.
The information we do have is:
- the first number in this sequence is 5
- the sum of the first six numbers is 120
Can you work out what the second number in the sequence is?

Need a hint?
- Remember that you always add the same amount to get to the next number in the sequence.
- Don't forget that each number is made by adding an amount to five.
- Try using algebraThe part of mathematics that deals with generalised arithmetic. Letters are used to represent variables and unknown numbers and to state general properties. to make an equation.
Solution
Worked out the answer? Here's how you can do it.
How did you get on with the sequences problem?
Let's look at the answers together.
Part A.
For Part A, we had a simple sequence starting with three and adding four each time: three, seven, eleven, fifteen, nineteenā¦
We had to figure it out what the first six numbers of this sequence add up to.
The sixth number in this sequence is twenty three because we're adding four each time.
So the sum is three plus seven plus eleven plus fifteen plus nineteen plus twenty three, which equals seventy eight.
Anybody got any good ideas about what we could do?
Part B.
Now, we've been given a different sequence of the same type. We know the first number in the sequence is five and the sum of the first six numbers is one hundred and twenty and we had to work out the second number in the sequence.
We could use algebra to find the solution. If the first number is five and we call the amount we add on each time 'd' then the second number is five plus d, the third number is five plus two d, etc.
The sum of the six numbers is five plus five plus d plus five plus two d plus five plus three d plus five plus four d plus five plus five d, which is thirty plus fifteen d, but we know that this sum is one hundred twenty, so thirty plus fifteen d equals one hundred and twenty.We could take thirty from each side, leaving fifteen d equals ninety.
Now, we can divide each side by fifteen to work out that d equals six. We know the second number in the sequence is five plus d and now we know what the value of d is so we can work out that that second number is five plus six, which is eleven.
Great work.
Part A

For Part A, our sequence starts with \(3\) and increases by \(4\) each time.
The first five numbers are \(3, 7, 11, 15, 19\).
To work out what the first six numbers add up to, we can work out the sixth number, and then add them all together.
\(\text{sixth number}=19+4=23\)
\(\text{total of first six numbers}=3+7+11+15+19+23=78\)
So the answer to Part A is 78.

Part B

For Part B, we need to work out the second number in a sequence.
We know:
- the first number if \(5\)
- the first six numbers add up to \(120\)
We donāt know:
- the second, third, fourth, fifth and sixth numbers
- how much the numbers increase by each time
We can find these out using algebraThe part of mathematics that deals with generalised arithmetic. Letters are used to represent variables and unknown numbers and to state general properties..
The increase is the same each time. Letās call the increase \(d\).


The first number is \(5\), so the other numbers are a combination of \(5\) plus one or more times \(d\):
\(\text{1st number}=5\)
\(\text{2nd number}=5+d\)
\(\text{3rd number}=5+2d\)
\(\text{4th number}=5+3d\)
\(\text{5th number}=5+4d\)
\(\text{6th number}=5+5d\)
All these numbers add up to \(120\):
\(5+5+d+5+2d+5+3d+5+4d+5+5d=120\)

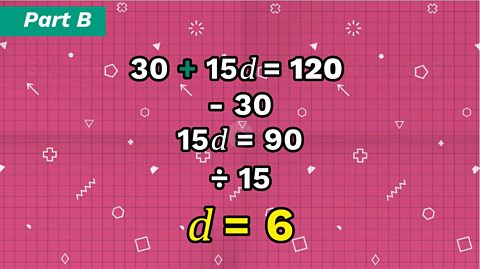
Simplify the equation:
\(30 +15d=120\)
Subtract \(30\) from each side:
\(15d=90\)
Divide both sides by \(15\):
\(d=6\)
We know the second number in the sequence is \(5+d\):
\(5+d = 5+6 =11\)
The answer to Part B is 11.
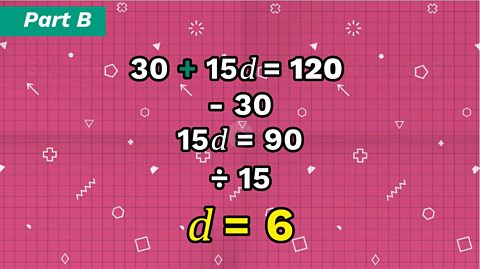
Maths Week Scotland 2023. listMaths Week Scotland 2023
Try out all the daily challenges from Maths Week Scotland 2023.

Maths Week Scotland 2022. listMaths Week Scotland 2022
Try out all the daily challenges from Maths Week Scotland 2022.

Maths Week Scotland 2021. listMaths Week Scotland 2021
Want more maths challenges? Here are all the problems from 2021.

More on Problem solving
Find out more by working through a topic
- count7 of 21

- count8 of 21

- count9 of 21

- count10 of 21