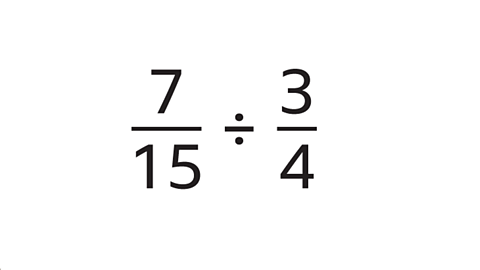Key points
- It can be useful to order a group of numbers by their value. Fractions can be arranged in Arranged from least value to greatest value. or Arranged from greatest value to least value. order.
- When fractions have the same Number written on the bottom of a fraction. The denominator is the number of equal parts. Eg, for 1⁄3, the denominator is 3, the Number written at the top of a fraction. The numerator is the number of parts used. Eg, for 1⁄3, the numerator is 1 are compared. The greater the numerator, the greater the fraction.
- When fractions have the same numerators, the denominators are compared. The greater the denominator, the smaller the fraction.
- When fractions have different numerators and denominators, they are rewritten as A fraction with the same value as another. with A denominator that is the same for two or more fractions. . The denominators then match. The numerators are compared to order the fractions.
- Learning about equivalent fractions is a useful skill for ordering fractions.
Ordering fractions with the same denominator
When fractions have the same Number written on the bottom of a fraction. The denominator is the number of equal parts. Eg, for 1⁄3, the denominator is 3, they are ordered by the size of their numerators:
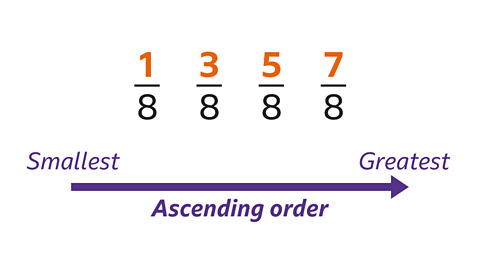
- The fraction with the smallest numerator is the smallest fraction.
- The fraction with the greatest numerator is the greatest fraction.
- Fractions can be arranged in Arranged from least value to greatest value. or Arranged from greatest value to least value. order. Ascending order starts with the smallest value and ascends to the greatest value. Descending order starts with the greatest value and descends to the smallest value.
- Two fractions can be compared in size using The symbol > is used when a value is greater than another, eg 23 > 5. The symbol < is used when a value is less than another, eg 11< 40
Examples
Image caption, Arrange these fractions in ascending and descending order.
1 of 6
Question
Arrange the fractions in ascending order. You might need a pen and paper to do this.
\( \frac{5}{8} \frac{1}{8} \frac{7}{8} \frac{3}{8} \)
Each fraction has the same denominator. Use the numerators to order the fractions. The smaller the numerator, the smaller the fraction.
Ordering fractions with the same numerators
To order fractions with the same Number written at the top of a fraction. The numerator is the number of parts used. Eg, for 1⁄3, the numerator is 1, the fractions are ordered by the size of their denominators.
- The fraction with the smallest denominator is the greatest fraction.
- The fraction with the greatest denominator is the smallest fraction.
- A A fraction that has 1 as the numerator and whose denominator is a non-zero integer, such as ½ and ⅓ has a numerator of 1. Unit fractions are also ordered using their denominators.
- Fractions may be arranged in Arranged from least value to greatest value. or Arranged from greatest value to least value. order.
Examples
Image caption, Which is smaller - 4⁄9 or 4⁄11?
1 of 7
Question
Arrange the fractions in descending order. You might need a pen and paper to do this.
\( \frac{5}{11} \frac{5}{7} \frac{5}{6} \frac{5}{8} \)
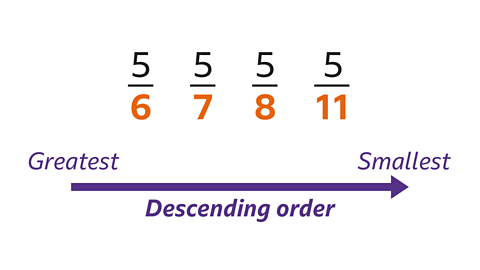
Use the denominators to order the fractions. The smaller the denominator, the greater the fraction.
Ordering fractions with different denominators and numerators
To order fractions with different denominators and numerators, the denominators have to be the same. To do this:
Find the The lowest multiple that is common to two or more numbers. The LCM of 15 and 12 is 60 because it is the lowest value in both of their multiplication tables. Also known as the least common multiple. of the denominators. This will be the denominator of the equivalent fractions.
Create the A fraction with the same value as another. by multiplying the numerator and denominator by the same value. The equivalent fractions should have the same denominators.
Compare the equivalent fractions using their numerators. The greater the numerator, the greater the fraction.
Write the original fractions in order, or compare the original fractions using The symbol > is used when a value is greater than another, eg 23 > 5. The symbol < is used when a value is less than another, eg 11< 40 symbols.
Examples
Image caption, Fractions with different denominators have to be rewritten as equivalent fractions to be able to compare them.
1 of 8
Practise ordering fractions
Activity
Arrange the fractions with the same numerators in ascending order.
Quiz
Practise what you've learned about ordering fractions with this quiz. You may need a pen and paper to help you work out the answers.
Real-world maths
Shades of paint can be compared by ordering fractions. A paint colour that is \( \frac{1}{3} \) blue and \( \frac{2}{3} \) white will be darker than a paint that is \( \frac{1}{5} \) blue and \( \frac{4}{5} \) white. This is because the fraction of blue paint is greater.
When shopping online being able to compare discounts that involve fractions can be helpful. For example, a £15 jumper is cheaper if there is \( \frac{1}{3} \) off (£5 off) compared to a reduction of \( \frac{1}{4} \) (reduced by £3.75).
Game - Divided Islands
Play the Divided Islands game! game
Using your maths skills, help to build bridges and bring light back to the islands in this free game from ý Bitesize.
More on Fractions
Find out more by working through a topic
- count6 of 14
- count7 of 14
- count8 of 14
- count9 of 14
